TULISAN MINGGU KE 2

1.     Metode antrian

Contoh.

Sebuah mesin layanan mempunyai waktu standby sesegera setelah melakukan

kegagalan. Waktu antar kegagalan atau standby terdistribusi eksponensial dengan

mean 10 jam. Kegagalan terjadi dengan laju 0.1 kejadian per jam. 

Hitunglah berapa :

a. Peluang terjadi kegagalan dalam 5 jam.

b. Peluang kegagalan terjadi setelah 6 jam dari sekarang dimana kegagalan

sebelumnya terjadi 3 jam lebih awal

c. Peluang tidak adanya kegagalan yang terjadi dalam periode 1-hari (24 jam)

Jawaban :

Distribusi eksponensial atas waktu antar kegagalan tersebut diberikan oleh

𝑓 𝑡 = 0.1𝑒−0.1𝑡, 𝑡 > 0

dimana distribusi poisson atas banyaknya kegagalan selama T periode diberikan oleh

𝑝𝑛𝑇 =0.1𝑇𝑛 𝑒−0.1𝑇𝑛!, 𝑛 = 0,1,2, …

a. Peluang kegagalan terjadi dalam 5 jam adalah

𝑃 𝑋 < 5 = 𝑓(𝑡)50𝑑𝑡 = 1 − 𝑒−0.5 = 0.393

b. peluang kegagalan terjadi setelah 6 jam dari sekarang dimana kegagalan

sebelumnya terjadi 3 jam lebih awal, maka digunakan Sifat forgetfullness atas

eksponensial

𝑃 X > 9 | 𝑡 > 3 = 𝑝 𝑡 > 6 = 𝑒−0.1 x 6 = 0.549

c. peluang tidak adanya kegagalan yang terjadi dalam periode 1-hari (24 jam),

yaitu

𝑝024 =. 1 x 240 𝑒−.1 x 240!= 𝑒−2.4 = 0.0919

Hal ini sama halnya dengan mengatakan bahwa 𝑝0

24 ekuivalen dengan waktu antar

kegagalan paling tidak dalam 24 jam, yaitu

𝑃 𝑋 > 24 = 0.1𝑒−0.1𝑡∞24𝑑𝑡 = 𝑒−2.4

2. Peramalan/forcasting

Contoh soal:

PT. Aroma Chocolate adalah sebuah perusahaan yang

menghasilkan permen coklat yang berkwalitas tinggi. Peningkatan

permintaan permen coklat untuk luar negeri maupun dalam negeri

sangatlah dipengaruh oleh kemampuan perusahaan tersebut dalam

mengirim pesanan dengan tepat waktu sehingga mampu memperoleh

pelanggan yang baru dan mempertahankan pelanggan yang lama.

Manajer telah mengumpulan data untuk 8 bulan terakhir yaitu :

Bulan                                                            Pesanan tiap bulan

Januari                                                                  100

Februari                                                                130

Maret                                                                     75

April                                                                     120

Mei                                                                       90

Juni                                                                      90

Juli                                                                       110

Agutus                                                                  75

Hitunglah rata-rata bergerak sederhana untuk 3 bulan terakhiri?

Penyelesaian :

Seringkali teknik rata-rata bergerak sederhana (simple moving

avarange) Dihitung untuk tiga kali periode, sehingga :

Rata-rata bergerak Maret = 90 + 110 +75

                                                3

                                      = 91,6 pesanan/bulan

Jadi rata-rata bergerak sederhana (simple moving avarange) untuk 3

bulan terakhir 91,6 pesanan/bulan.

2.2. Metode Rata-Rata Tertimbang

Rata-rata dengan bobot atau kepentingan dari setiap data berbeda. Besar

dan kecilnya bobot tergantung pada alasan ekonomi dan teknisnya. 5

Metode rata-rata bergerak sederhana menggunakan bobot yang sama

pada setiap periode. Hal ini menunjukkan bentuk prakiraannya linier.

Dalam banyak hal periode yang diramalkan (periode t + 1) banyak

memiliki keadaan yang sama dengan periode t di bandingkan periode

yang lain, misalnya t-1 atau t-2 oleh karena itu, periode terakhir

seyoigianya mendapat bobot yang lebih besar di bandingkan dengan

periode sebelumnya (disini menyiratkan adanya bentuk prakiraan yang

non-linier). Metode rata-rata tertimbang (weigted moving average) juga

menggunakan data N periode terakhir sebagai data historis untuk

melakukan prakiraan, tetapi setiap periode mendapat bobot yang

berbeda. Metode rata-rata tertimbang mempunyai kelemahan yaitu:

Metode ini tidak dapat menanggulangi dengan baik adanya trend atau

musiman, walaupun metode ini lebih disbanding rata-rata total selain

itu Metode ini memerlukan penyimpanan yang lebih banyak karena

semua T pengamatan terakhir harus disimpan, tidak hanya nilai

tengahnya. Sedangkan kelebihannya Kelebihan dari metode rata-rata

tertimbang yaitu dapat mengetahui/melihat secara langsung

perbedaan keadaan pada setiap periode yang diramalkan, seperti

perbedaan keadaan pada periode t dibandingkan dengan periode yang lain seperti periode t-1 atau t-2.

3. Linear programing

Seorang pedagang sepeda ingin membeli 25 sepeda untuk persediaan. Ia ingin membeli sepeda gunung dengan harga Rp 1.500.000,00 per buah dan sepeda balap dengan harga Rp 2.000.000,00 per buah. Ia berencana tidak akan mengeluarkan uang lebih dari Rp 42.000.000,00. Jika keuntungan sebuah sepeda gunung Rp 500.000,00 dan sebuah sepeda balap Rp 600.000,00, maka keuntungan maksimum yang diterima pedagang adalah …

Pembahasan Tanpa membuat tabel, kita dapat memodelkan kendala-kendala dari permasalahan tersebut sebagai berikut.

x + y ≤ 25,
1.500.000x + 2.000.000y ≤ 42.000.000,
x ≥ 0, y ≥ 0,
x dan y bilangan cacah.

Dengan fungsi objektifnya adalah f(x, y) = 500.000x + 600.000y. Sehingga apabila digambarkan, daerah selesaiannya akan nampak seperti berikut.

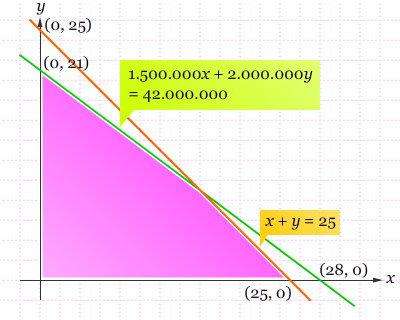
Selanjutnya kita tentukan titik potong grafik persamaan 1.500.000x + 2.000.000y = 42.000.000 dan x + y = 25.

Sehingga,

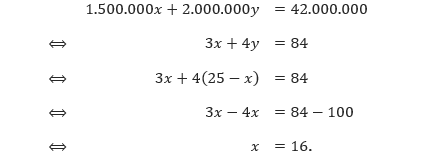
Diperoleh,

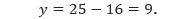
Selanjutnya kita lakukan uji titik pojok ke dalam fungsi objektifnya.

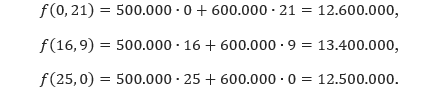
Jadi, keuntungan maksimum yang diterima pedagang adalah Rp 13.400.000,00.

SUMBER :

https://yos3prens.wordpress.com/2013/10/02/10-soal-dan-pembahasan-permasalahan-proram-linear/

http://staff.uny.ac.id/sites/default/files/pendidikan/Nikenasih%20Binatari,%20S.Si.,%20M.Si./MODUL%20PRAKTIKUM%20TEORI%20ANTRIAN%20-%20FIX%20terakhir.pdf

http://repository.unhas.ac.id/bitstream/handle/123456789/13332/PERAMALAN.pdf?sequence=1